Example¶
Problem description¶
This is a classical example introduced by Simo and Vu-Quoc, (1988) and it involves extremely large displacements and rotations and served later also for the demonstration of numerical stability of energy preserving algorithms. The beam lies initially inclined in \(XZ\)-plane and is subjected at the lower end to point force \(f_{x}\) and point moments \(h_{y}\) and \(h_{z}\) with constant direction and piecewise linear magnitude in time as shown in the figure.
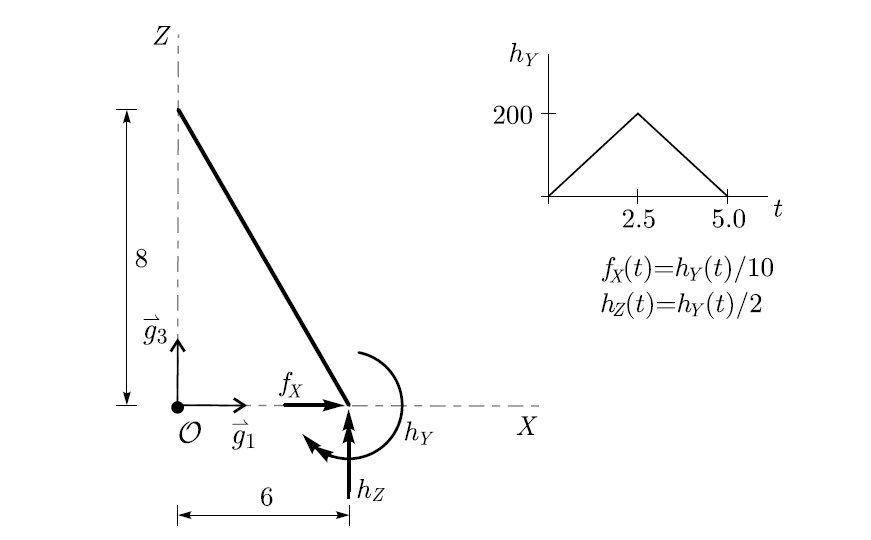
Figure 1. Free flight of a flexible beam¶
At \(t = 5\), the point loads vanish leaving the beam to fly in free motion until the chosen final time. The remaining parameters of the beam are: \(EA = GA_{2} = GA_{3} = 10000\), \(GI_{1} = EI_{2} = EI_{3} = 500\), \(\rho A = 1, \boldsymbol{J}_{\rho} = \text{diag}[10, 10, 10]\).